以前製作した 簡易FANコントローラは 静かに稼働している。 ただ、未だケースを作成できていない。 設計したもののサイズが大きくなり作成していない。 サイズ確認用のパネルに固定した状態で使用を続けている。
PWMを絞りきってもFANの回転が止まらなかったので 電源SWもつけているのが敗因かもしれないと SW付きVRを購入したがユニバーサル基板に刺さらないことが判明。 そこで基板を起こしてコンパクトなコントローラにすることにしたが 気になることが出てきた。PWM回路の直線性は大丈夫だろうか？
PWM信号発生回路の直線性電子工作
2022年4月6日水曜日
発振波形の式
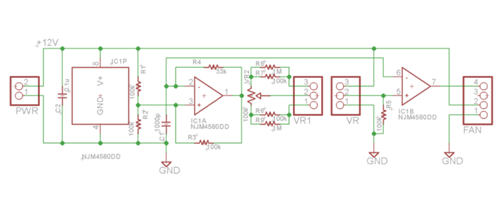
PWM信号発生回路を以下に示す。
|
コンデンサc1(1000pF)は R4(33kΩ)を介して電源電圧$V$(12V)への充電と 0Vへの放電を繰り返す。 切り替わりの電圧は$\frac{1}{3}V$の4Vと $\frac{2}{3}V$の8V。
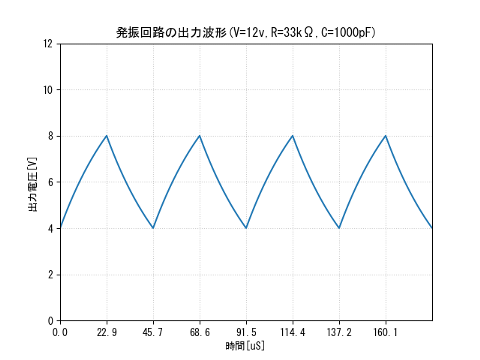
$\frac{1}{3}V$からの立ち上がりの波形は、 経過時間を$t_1$とすると出力電圧$v$は \begin{equation} \label{v1} v = V(1 - \frac{2}{3}e^{-\frac{t_1}{T}}) \tag{1} \end{equation} ここで $V$は電源電圧、$T$は時定数で \[ T = rc \] $\frac{2}{3}V$からの立ち下がりは、 立ち下がりからの経過時間を$t_2$とすると \begin{equation} \label{v2} v = \frac{2}{3}Ve^{-\frac{t_2}{T}} \tag{2} \end{equation} 波形の周期を$T_p$とすると $t_1 = \frac{T_p}{2}$で $v = \frac{2}{3}V$となるので 式\eqref{v1}に代入すると \begin{eqnarray*} \frac{2}{3}V & = & V(1-\frac{2}{3}e^{-\frac{T_p}{2T}}) \\ e^{-\frac{T_p}{2T}} & = & \frac{1}{2}\\ \frac{-T_p}{2T} & = & \ln(\frac{1}{2})\\ \end{eqnarray*} \begin{equation} \label{tp} T_p = 2\ln 2 \; T \simeq 1.386 T \tag{3} \end{equation} これらの式から波形を計算すると 以下の図の波形が得られる。
 |
PWM回路の直線性
発振回路の出力とVRの電圧をコンパレータで比較してPWM信号を出力する。 VRの電圧に対するPWMのパルス幅の変化、直線性を調べたい。 VRの電圧を$v_c$として 発振回路の出力電圧が$v_c$よりも大きくなる時間$T_h$を求めたい。 式\ref{v1}を $t_1$について解くと \begin{equation} \label{t1} t_1 = -T\ln( \frac{3}{2}(1-\frac{v}{V})) \tag{4} \end{equation} 式\ref{v2}を$t_2$について解くと \begin{equation} \label{t2} t_2 = -T\ln(\frac{3}{2} \cdot \frac{v}{V}) \tag{5} \end{equation} $v > v_c$となる時間 $T_h$は \begin{eqnarray*} T_h & = & \frac{T_p}{2} - t_1 + t_2 = &\frac{T_p}{2} + T \ln(\frac{3}{2}(1-\frac{v}{V})) - T\ln( \frac{3}{2}\cdot\frac{v}{V}) \\ \end{eqnarray*} 周期$T_p$中の$v > v_c$となる期間の割合$P$は \begin{eqnarray*} P & = & \frac{T_h}{T_p} & = & \frac{1}{2} + \frac{T}{T_p}(\ln(\frac{3}{2}(1-\frac{v}{V})) - \ln( \frac{3}{2}\cdot\frac{v}{V}) ) \\ \end{eqnarray*} 式\ref{tp}を代入すると \begin{equation} \label{p} P = \frac{1}{2} + \frac{1}{2\ln 2}(\ln(\frac{3}{2}(1-\frac{v}{V})) - \ln( \frac{3}{2}\cdot\frac{v}{V}) ) \tag{6} \end{equation} となる。
この式で$V$=12V, $v$を4～8Vの範囲で計算した結果のグラフを下に示す。
 |
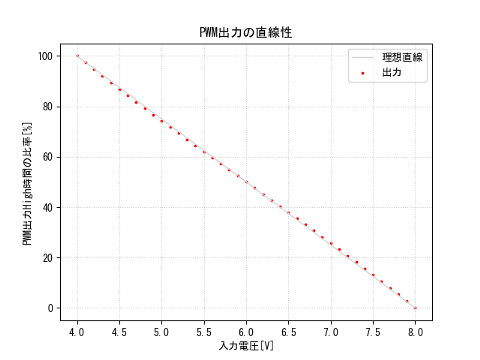赤い点が計算結果で、直線は (4V,100%)と(8V,0%)を結んだもので、 点がほとんど直線状に載っていることがわかる。
直線性誤差だけグラフ化すると次のようになる
 |
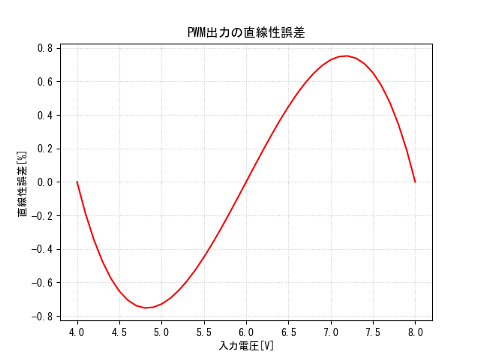最大でも 0.8% 程度に収まっていることがわかる。 計測用ならともかく、制御用としては十分すぎる直線性である。
最後に
これまでの回路で直線性に問題ないことがわかったので 安心して簡易FANコントローラの基板を起こすことができる。
今回は式を手できれいに書く自信がなかったので LaTeXで書きながら考えた。 そして mathplotlibでグラフ化し確認した。 mathplotlibはgnuplotをpython化したようなライブラリで gnuplotに慣れたものとしては大変使いやすい。 LaTeXの数式をwebに表示するために MathJax を使用した。 数式をきれいに表示できると やる気が出る。
